|
|
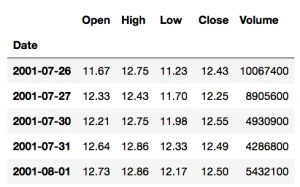
import numpy as np from pandas_datareader import data as wb import matplotlib.pyplot as plt AMZN = wb.DataReader('AMZN', data_source='google', start='2000-1-1') AMZN.head() |
|
|
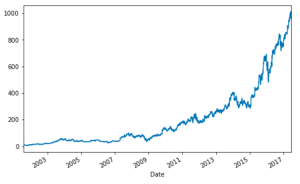
AMZN['Close'].plot(figsize=(8,5)) plt.show() |
Simple rate of return
rate of return = (ending price – beginning price) / beginning price
(P1 – P0) / P0 = P1 / P0 – 1
Use when dealing with multiple assets over the same timeframe.
|
|
AMZN['simple_return'] = (AMZN['Close'] / AMZN['Close'].shift(1)) - 1 print (AMZN['simple_return']) |
Date
2001-07-26 NaN
2001-07-27 -0.014481
2001-07-30 0.024490
2001-07-31 -0.004781
2001-08-01 0.000801
2001-08-02 -0.024800
2001-08-03 -0.003281
2001-08-06 -0.020576
2001-08-07 -0.025210
2001-08-08 -0.042241
2001-08-09 -0.058506
2001-08-10 -0.048757
2001-08-13 0.017085
2001-08-14 0.040514
2001-08-15 -0.042735
2001-08-16 -0.026786
2001-08-17 0.018349
2001-08-20 0.041041
2001-08-21 -0.049038
2001-08-22 0.031345
2001-08-23 -0.055882
2001-08-24 0.062305
2001-08-27 -0.009775
2001-08-28 -0.015795
2001-08-29 -0.078235
2001-08-30 -0.054407
2001-08-31 0.028769
2001-09-04 -0.039150
2001-09-05 -0.109430
2001-09-06 0.065359
…
2017-05-10 -0.004062
2017-05-11 -0.001402
2017-05-12 0.014489
2017-05-15 -0.003516
2017-05-16 0.008455
2017-05-17 -0.022058
2017-05-18 0.014533
2017-05-19 0.001408
2017-05-22 0.011283
2017-05-23 0.000896
2017-05-24 0.009068
2017-05-25 0.013291
2017-05-26 0.002416
2017-05-30 0.000924
2017-05-31 -0.002087
2017-06-01 0.001337
2017-06-02 0.010824
2017-06-05 0.004579
2017-06-06 -0.008246
2017-06-07 0.007049
2017-06-08 0.000198
2017-06-09 -0.031635
2017-06-12 -0.013697
2017-06-13 0.016457
2017-06-14 -0.004405
2017-06-15 -0.012596
2017-06-16 0.024415
2017-06-19 0.007553
2017-06-20 -0.002593
2017-06-21 0.009712
Name: simple_return, Length: 4000, dtype: float64
|
|
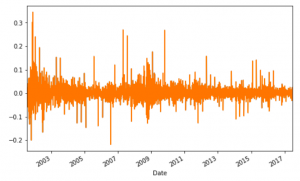
AMZN['simple_return'].plot(figsize=(8,5)) plt.show() |
|
|
avg_returns_d = AMZN['simple_return'].mean() avg_returns_d |
0.0015193424705951424
|
|
avg_returns_a = AMZN['simple_return'].mean() * 250 avg_returns_a |
0.3798356176487856
|
|
print (str(round(avg_returns_a, 5) * 100) + ' %') |
37.984 %
Logarithmic rate of return
ln(Pt / Pt-1)
10.0% = log $116 / $105 = log $116 – log $105
Use when you make calculations about a single asset over time.
|
|
AMZN['log_return'] = np.log(AMZN['Close'] / AMZN['Close'].shift(1)) print (AMZN['log_return']) |
Date
2001-07-27 NaN
2001-07-30 0.024195
2001-07-31 -0.004792
2001-08-01 0.000800
2001-08-02 -0.025113
2001-08-03 -0.003287
2001-08-06 -0.020791
2001-08-07 -0.025533
2001-08-08 -0.043159
2001-08-09 -0.060287
2001-08-10 -0.049986
2001-08-13 0.016941
2001-08-14 0.039715
2001-08-15 -0.043675
2001-08-16 -0.027151
2001-08-17 0.018182
2001-08-20 0.040221
2001-08-21 -0.050282
2001-08-22 0.030864
2001-08-23 -0.057504
2001-08-24 0.060441
2001-08-27 -0.009823
2001-08-28 -0.015921
2001-08-29 -0.081465
2001-08-30 -0.055943
2001-08-31 0.028363
2001-09-04 -0.039937
2001-09-05 -0.115893
2001-09-06 0.063312
2001-09-07 0.043224
…
2017-05-11 -0.001403
2017-05-12 0.014385
2017-05-15 -0.003522
2017-05-16 0.008420
2017-05-17 -0.022305
2017-05-18 0.014428
2017-05-19 0.001407
2017-05-22 0.011220
2017-05-23 0.000896
2017-05-24 0.009027
2017-05-25 0.013204
2017-05-26 0.002413
2017-05-30 0.000923
2017-05-31 -0.002089
2017-06-01 0.001336
2017-06-02 0.010766
2017-06-05 0.004569
2017-06-06 -0.008281
2017-06-07 0.007024
2017-06-08 0.000198
2017-06-09 -0.032146
2017-06-12 -0.013792
2017-06-13 0.016324
2017-06-14 -0.004414
2017-06-15 -0.012676
2017-06-16 0.024122
2017-06-19 0.007524
2017-06-20 -0.002596
2017-06-21 0.009665
2017-06-22 -0.000928
Name: log_return, dtype: float64
|
|
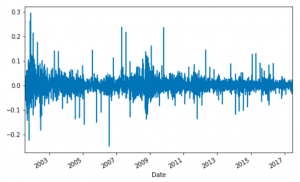
AMZN['log_return'].plot(figsize=(8, 5)) plt.show() |
|
|
log_return_d = AMZN['log_return'].mean() log_return_d |
0.0010977419081520047
|
|
log_return_a = AMZN['log_return'].mean() * 250 log_return_a |
0.2744354770380012
|
|
print (str(round(log_return_a, 5) * 100) + ' %') |
27.444 %
Monte Carlo simulations
We are interested in observing the different possible realizations of a future event.
– Scenario 1
– Scenario 2
– Scenario 3
– Scenario 4
– Scenario 5
– Scenario 6
Historical data => A larger data set with “fictional” data
Current Revenues = Last Year Revenues * (1 + y-o-y growth rate)
– Revenue growth rate – Historical Data or User Intuition
– Revenue volatility – Historical Data or User Intuition
Cogs (Cost of Goods Sold): Modeled as a percentage of revenues
Opex: Modeled as a percentage of revenues
Revenues – Cogs = Gross Profit
Revenues – Opex = Operating Profit
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import numpy as np import matplotlib.pyplot as plt rev_m = 170 rev_stdev = 20 iterations = 1000 rev = np.random.normal(rev_m, rev_stdev, iterations) rev plt.figure(figsize=(15,6)) plt.plot(rev) plt.show() COGS = - (rev * np.random.normal(0.6,0.1)) plt.figure(figsize=(15,6)) plt.plot(COGS) plt.show() COGS.mean() // -89.588838273282661 COGS.std() // 10.581370507673284 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Gross_Profit = rev + COGS Gross_Profit plt.figure(figsize=(15,6)) plt.plot(Gross_Profit) plt.show() max(Gross_Profit) // 111.04813446627591 min(Gross_Profit) // 52.352121850588489 Gross_Profit.mean() // 80.688398780785718 Gross_Profit.std() // 9.5301363387028868 plt.figure(figsize=(10,6)) plt.hist(Gross_Profit, bins =[40,50,60,70,80,90,100,110,120]) plt.show() plt.figure(figsize=(10,6)) plt.hist(Gross_Profit, bins =20) plt.show() |
Asset pricing with Monte Carlo
Price Today = Price Yesterday * er
r: log return of share price between yesterday and today.
In(price today / price yesterday)
e.g. eIn(x) = x
Price Today = Price Yesterday * e
Logarithm Basics
log2(16) = x
2x = 16
x = 4
log100(1) = 0
1000 = 1
log2(2) = 1/3
81/3 = 2
log2(1/8) = -3
2-3 = 1/8
log8(1/2) = -1/3
8-1/3 = 1/81/3 = 1/2
Brownian motion
We can use Brownian motion in order to model r:
– Drift:
=> The direction rates of return have been headed in the past.
In(Current Price / Previous Price)
=> Calculate average, standard deviation and variance of daily returns in the historical period.
Drift = (μ – 1/2σ2)
Drift is the expected daily return of the stock.
– Volatility:
Random variable.
Random variable = σ * Z(Rand(0;1))
Price Today = Price Yesterday * eDrift + Random variable
Repeat the calculation 1,000 times.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import pandas as pd from pandas_datareader import data as wb import matplotlib.pyplot as plt from scipy.stats import norm %matplotlib inline ticker = 'AMZN' data = pd.DataFrame() data[ticker] = wb.DataReader(ticker, data_source = 'google', start='2007-1-1')['Close'] log_returns = np.log(1+data.pct_change()) log_returns.tail() data.plot(figsize=(10,6)) log_returns.plot(figsize=(10,6)) u=log_returns.mean() u // AMZN 0.001228 // dtype: float64 var = log_returns.var() var // AMZN 0.000635 // dtype: float64 drift = u - (0.5*var) drift // AMZN 0.00091 // dtype: float64 stdev = log_returns.std() stdev // AMZN 0.025207 // dtype: float64 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
type(drift) // pandas.core.series.Series type(stdev) // pandas.core.series.Series np.array(drift) // array([ 0.0009102]) // object.values: transfers the object into a numpy array drift.values // array([ 0.0009102]) stdev.values // array([ 0.02520659]) norm.ppf(0.95) // 1.6448536269514722 x = np.random.rand(10,2) x norm.ppf(x) z = norm.ppf(np.random.rand(10,2)) z t_intervals = 1000 iterations = 10 daily_returns = np.exp(drift.values + stdev.values * norm.ppf(np.random.rand(t_intervals, iterations))) daily_returns |
Euler’s Method
Differential equations introduction
yII + 2yI = 3y
fII(x) + 2fI(x) = 3f(x)
Leibniz’s notation
d2y / dx2 + 2 (dy / dx) = 3y
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
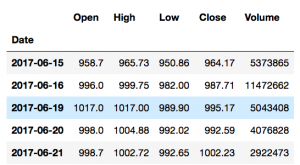
S0 = data.iloc[-1] S0 // AMZN 995.17 // Name: 2017-06-19 00:00:00, dtype: float64 price_list = np.zeros_like(daily_returns) price_list price_list[0] = 50 price_list for t in range(1, t_intervals): price_list[t] = price_list[t - 1]*daily_returns[t] price_list plt.figure(figsize=(10,6)) plt.plot(price_list) |
An Introduction to Derivative Contracts
A derivative is a financial instrument, whose price is derived based on the development of one or more underlying assets.
Originally, derivatives served as a hedging instrument.
– Hedging
– Speculating
– Aribtrageurs
Four Types of derivatives
– Forwards
Two parties agree that one party will sell to the other an underlying asset at a future point of time.
– Futures
Highly standardized forward contracts.
– Swaps
Two parties agree to exchange cash flows based on an underlying asset.
e.g. Interest rate, Stock Price, Bond Price, Commodity
– Options
An option contract enables its owner to buy or sell an underlying asset at a given price.
The Black Scholes formula
– A tool for derivatives pricing.
– calculates the value of an option.
– The holder of the option may decide he wants to buy the stock, but he may also decide he is better off without doing it. This freedom is valuable to every investor. Hence, it has a price.
A Call Option’s Payoff
– Strike Price vs. Share Price
– Share Price > Strike Price –> Exercise
– Strike Price > Share Price –> Don’t Exercise
The Black Scholes Formula
The Black Scholes formula calculates the value of a call by taking the difference between the amount you get if you exercise the option minus the amount you have to pay if you exercise the option.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import numpy as np import pandas as pd from pandas_datareader import data as wb from scipy.stats import norm def d1(S, K, r, stdev, T): return (np.log(S / K) + (r - stdev ** 2/2) * T) / (stdev * np.sqrt(T)) def d2(S, K, r, stdev, T): return (np.log(S / K) + (r - stdev ** 2/2) * T) / (stdev * np.sqrt(T)) norm.cdf(0) // 0.5 norm.cdf(0.25) // 0.5987063256829237 norm.cdf(0.75) // 0.77337264762313174 norm.cdf(9) // 1.0 def BSM(S, K, r, stdev, T): return (S*norm.cdf(d1(S, K, r, stdev, T))) - (K * np.exp(-r * T) * norm.cdf(d2(S, K, r, stdev, T))) ticker = 'AMZN' data = pd.DataFrame() data[ticker] = wb.DataReader(ticker, data_source='google', start='2007-1-1', end='2017-3-21')['Close'] S = data.iloc[-1] S // AMZN 843.2 // Name: 2017-03-21 00:00:00, dtype: float64 log_returns = np.log(1+data.pct_change()) stdev = log_returns.std()*250**0.5 stdev // AMZN 0.402353 // dtype: float64 r = 0.025 K = 110.0 T = 1 d1(S, K, r, stdev, T) // AMZN 4.922989 // dtype: float64 d2(S, K, r, stdev, T) // AMZN 4.922989 // dtype: float64 BSM(S, K, r, stdev, T) // AMZN 735.915596 // Name: 2017-03-21 00:00:00, dtype: float64 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import numpy as np import pandas as pd from pandas_datareader import data as wb from scipy.stats import norm import matplotlib.pyplot as plt %matplotlib inline ticker = 'AMZN' data = pd.DataFrame() data[ticker] = wb.DataReader(ticker, data_source='google', start='2007-1-1', end='2007-3-21')['Close'] log_returns = np.log(1 + data.pct_change()) r = 0.025 stdev = log_returns.std() * 250 ** 0.5 stdev // AMZN 0.28593 // dtype: float64 type(stdev) // pandas.core.series.Series stdev = stdev.values stdev // array([ 0.28592956]) T=1.0 t_intervals = 250 delta_t = T / t_intervals iterations = 10000 Z = np.random.standard_normal((t_intervals + 1, iterations)) S = np.zeros_like(Z) S0 = data.iloc[-1] S[0] = S0 for t in range(1, t_intervals + 1): S[t]=S[t-1] * np.exp((r - 0.5 * stdev ** 2) * delta_t + stdev * delta_t ** 0.5 * Z[t]) S S.shape // (251, 10000) plt.figure(figsize=(10,6)) plt.plot(S[:,:10]) |
|
|
p = np.maximum(S[-1] - 110, 0) p // array([ 0., 0., 0., ..., 0., 0., 0.]) p.shape // (10000,) C = np.exp(-r * T) * np.sum(p) / iterations C // 0.0 |
Multivariate Regressions
Yi = β0 + β1X1 + β2X2 + βiXi + εi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np import pandas as pd from scipy import stats import statsmodels.api as sm import matplotlib.pyplot as plt data = pd.read_excel('[PATH]/Housing.xlsx') data // Multivariate Regression: // Independent Variables: "House Size (sq.ft.)", "Number of Rooms", "Year of Construction" X = data[['House Size (sq.ft.)', 'Number of Rooms', 'Year of Construction']] Y = data['House Price'] X1 = sm.add_constant(X) reg = sm.OLS(Y,X1).fit() reg.summary() // Independent Variables: 'House Size (sq.ft.)', 'Number of Rooms' X = data[['House Size (sq.ft.)', 'Number of Rooms']] Y = data['House Price'] X1 = sm.add_constant(X) reg = sm.OLS(Y, X1).fit() reg.summary() |
The Capital Asset Pricing Model (CAPM)
According to Markowitz, in the CAPM investors are:
– risk-averse
– prefer higher returns
– willing to buy the optimal portfolio
The market portfolio:
– a combination of all the possible investments in the world.
The risk-free asset:
– the CAPM assumes the existence of a risk-free asset.
– an investment with zero risk.
– Why should we assume the risk-free rate has a lower expected rate of return?
=> In efficient markets, investors are only compensated for the added risk they are willing to bear.
The Capital Market Line
– investors will allocate their money between the risk-free and the market portfolio
In the CAPM, investors will invest in:
– depending on their risk preferences, they will choose to buy more of the risk-free asset or more of the market portfolio.
Beta
β = Cov(rx, rm) / σm2
– measures the market risk that cannot be avoided through diversification.
β = 0: No relationship
β < 1: Defensive (Walmart)
β > 1: Aggressive (Ford)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import numpy as np import pandas as pd from pandas_datareader import data as wb tickers = ['AMZN','S&P 500'] data = pd.DataFrame() for t in tickers: data[t] = wb.DataReader(t, data_source='google', start='2012-1-1',end='2016-12-31')['Close'] sec_returns = np.log(data/data.shift(1)) cov = sec_returns.cov() * 250 cov cov_with_market = cov.iloc[0,1] cov_with_market // 0.0039599527224196103 market_var = sec_returns['S&P 500'].var() * 250 market_var // 0.02393760982543131 // Beta: AMZN_beta = cov_with_market / market_var AMZN_beta // 0.16542807537169221 |
The Capital Asset Pricing Model
ri = rf + βim(rm – rf)
rf: risk-free
βim: beta between the stock and the market
rm: market return
Risk-free: Approximate with 10-year US government bond yield: 2.5%
Beta: Approximate the market portfolio with the S&P500: 0.62
Equity Risk Premium: Historically, it has been between 4.5% and 5.5%
r(i) = 2.5% + 0.62 * 5% = 5.6%
|
|
// Calculate the expected return of AMZN(CAPM): AMZN_er = 0.025 + AMZN_beta * 0.05 AMZN_er // 0.033271403768584611 |
Sharpe Ratio
William Sharpe
Sharpe Ratio = (ri – rf) / σi
rf: risk-free rate
ri: rate of return of the stock “i”
σi: standard deviation of the stock “i”
|
|
// Sharpe ratio: Sharpe = (AMZN_er - 0.025) / (sec_returns['AMZN'].std() * 250 ** 0.5) Sharpe // 0.02701837714000498 |
Alpha
The Capital Asset Pricing Model:
ri = α + rf + βim(rm – rf)
– The standard CAPM setting assumes an alpha equal to 0.
– We can only compare the alpha of investments with a similar risk profile.
Portfolio Theory
1952, Harry Markowitz published a paper.
– investors should understand the relationship between securities in their portfolio.
Implementation
|
|
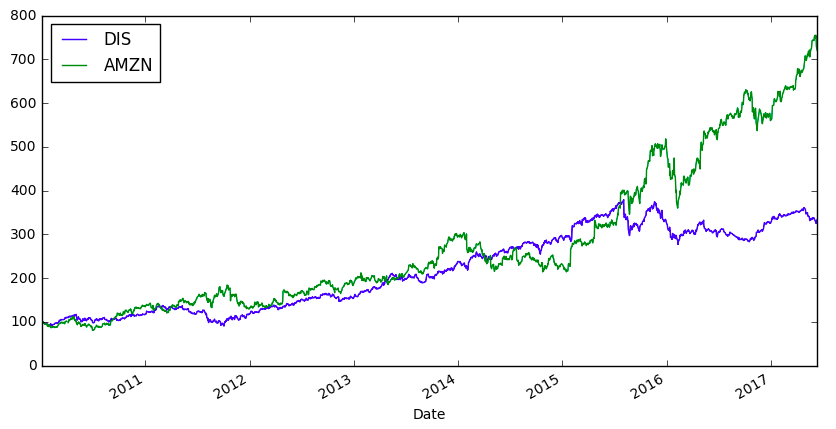
import numpy as np import pandas as pd from pandas_datareader import data as wb import matplotlib.pyplot as plt %matplotlib inline assets = ['DIS', 'AMZN'] pf_data = pd.DataFrame() for a in assets: pf_data[a] = wb.DataReader(a, data_source = 'google', start = '2010-1-1')['Close'] pf_data.tail() (pf_data / pf_data.iloc[0] * 100).plot(figsize=(10,5)) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
log_returns = np.log(pf_data / pf_data.shift(1)) log_returns.mean() * 250 // DIS 0.160962 // AMZN 0.268312 // dtype: float64 log_returns.cov() * 250 log_returns.corr() num_assets = len(assets) num_assets // 2 arr = np.random.random(2) arr // array([ 0.52831474, 0.47945205]) arr[0] + arr[1] // 1.0077667888401995 weights = np.random.random(num_assets) weights /= np.sum(weights) weights // array([ 0.47348175, 0.52651825]) weights[0] + weights[1] // 1.0 |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
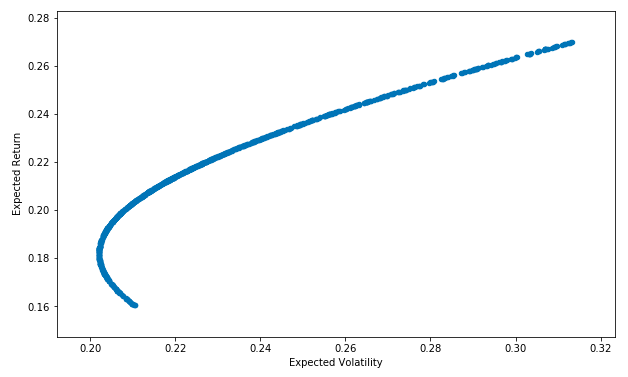
// Expected Portfolio Return: np.sum(weights * log_returns.mean()) * 250 // 0.2496822910761077 // Expected Portfolio Variance: np.dot(weights.T, np.dot(log_returns.cov() * 250, weights)) // 0.074759086518318432 // Expected Portfolio Volatility: np.sqrt(np.dot(weights.T,np.dot(log_returns.cov() * 250, weights))) // 0.27342107914043212 pfolio_returns = [] pfolio_volatilities = [] for x in range (1000): weights = np.random.random(num_assets) weights /= np.sum(weights) pfolio_returns.append(np.sum(weights * log_returns.mean()) * 250) pfolio_volatilities.append(np.sqrt(np.dot(weights.T,np.dot(log_returns.cov() * 250, weights)))) pfolio_returns, pfolio_volatilities pfolio_returns = [] pfolio_volatilities = [] for x in range (1000): weights = np.random.random(num_assets) weights /= np.sum(weights) pfolio_returns.append(np.sum(weights * log_returns.mean()) * 250) pfolio_volatilities.append(np.sqrt(np.dot(weights.T,np.dot(log_returns.cov() * 250, weights)))) pfolio_returns = np.array(pfolio_returns) pfolio_volatilities = np.array(pfolio_volatilities) pfolio_returns, pfolio_volatilities portfolios = pd.DataFrame({'Return': pfolio_returns, 'Volatility': pfolio_volatilities}) portfolios.head() portfolios.tail() portfolios.plot(x='Volatility', y='Return', kind='scatter', figsize=(10,6)); plt.xlabel('Expected Volatility') plt.ylabel('Expected Return') |