Mastering Bitcoin: Unlocking Digital Cryptocurrencies
The summary of ‘7. The Blockchain’
from Mastering Bitcoin: Unlocking Digital Cryptocurrencies
by Andreas M. Antonopoulos.
Introduction
The blockchain is back-linked list of transactions. Bitcoin uses Google’s LevelDB. The first block serves as the foundation of the stack
Each block is identified by a hash generated by SHA256 algorithm & has the parent’s hash. The chain goes back to its first, genesis block
A block can have multiple children (“fork”) when different blocks are discovered simultaneously by different miners. But it’s temporal
Each block has its previous block’s hash. The cascade effect makes it immutable because it’s impossible to recalculate all subsequent blocks
While the possibility of any block being reversed always exists, it decreases as time passes like layers in a geological formation
Structure of a Block
A block is a container data structure made of: 1) a header (80 bytes); 2) transactions (avg 250 bytes x 500)
Table 7-1. The structure of a block
Block Header
A header consists of: 1) reference to a previous block hash; 2) difficulty, timestamp & nonce; 3) merkle tree root (summary of transactions)
Table 7-2. The structure of the block header
Block Identifiers: Block Header Hash and Block Height
The identifier of a block: 1) The 32-byte “block hash” made by hashing the block header twice through SHA256 algorithm
The block hash is not included inside the block’s data structure & might be stored in a separate database as part of the block’s metadata
2) the block height: the first block’s height is 0. Each subsequent block is one position “higher” in the blockchain. (278,000 in Jan 2014)
Unlike the block hash, the block height does not always identify a single block. Two or more blocks might have the same block height (fork)
The Genesis Block
The genesis block: the first block in the blockchain created in 2009. It is the common ancestor of all the blocks in the blockchain
The genesis block is statically encoded within the bitcoin client software & cannot be altered
The following identifier hash belongs to the genesis block:
|
1 |
000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f |
Using the Bitcoin Core reference client on the command line:
|
1 |
$ bitcoind getblock 000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f |
The bitcoin node then receives a new block from the network, which it parses as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
{ "hash" : "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f", "confirmations" : 308321, "size" : 285, "height" : 0, "version" : 1, "merkleroot" : "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b", "tx" : [ "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b" ], "time" : 1231006505, "nonce" : 2083236893, "bits" : "1d00ffff", "difficulty" : 1.00000000, "nextblockhash" : "00000000839a8e6886ab5951d76f411475428afc90947ee320161bbf18eb6048" } |
The hidden message in genesis block: “The Times 03/Jan/2009 Chancellor on brink of second bailout for banks.”
Linking Blocks in the Blockchain
As a node receives incoming blocks from the network, it will validate these blocks and then link them to the existing blockchain
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
{ "size" : 43560, "version" : 2, "previousblockhash" : "00000000000000027e7ba6fe7bad39faf3b5a83daed765f05f7d1b71a1632249", "merkleroot" : "5e049f4030e0ab2debb92378f53c0a6e09548aea083f3ab25e1d94ea1155e29d", "time" : 1388185038, "difficulty" : 1180923195.25802612, "nonce" : 4215469401, "tx" : [ "257e7497fb8bc68421eb2c7b699dbab234831600e7352f0d9e6522c7cf3f6c77", #[... many more transactions omitted ...] "05cfd38f6ae6aa83674cc99e4d75a1458c165b7ab84725eda41d018a09176634" ] } |
A node in the local copy 1) receives a new block from the network 2) finds it’s a child of the last block 3) adds it to the end of the chain
Merkle Trees
A merkle tree, a binary hash tree, efficiently summarizes and verifies the integrity of all the transactions in the block
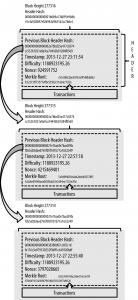
Figure 7-1. Blocks linked in a chain, by reference to the previous block header hash
A Merkle tree is constructed by recursively hashing pairs of nodes until there is only one hash, called the root, or merkle root
We start with four transactions, A, B, C & D (Fig 7-2) whose data is hashed & the resulting hash is stored in each node as HA, HB, HC, & HD:
|
1 |
H~A~ = SHA256(SHA256(Transaction A)) |
To construct the parent node HAB, the two 32-byte hashes of the children are concatenated to create a 64-byte string which is double-hashed:
|
1 |
H~AB~ = SHA256(SHA256(H~A~ + H~B~)) |
This process continues until there is one 32-byte node, the Merkle root, which is stored in the block header & summarizes all transactions
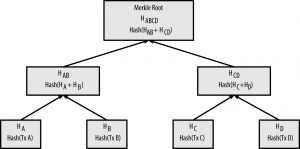
Figure 7-2. Calculating the nodes in a merkle tree
A binary tree needs an even number of nodes. If there is an odd number of them, the last hash will be duplicated: a balanced tree (Fig 7-3)
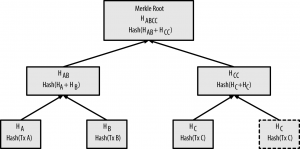
Figure 7-3. Duplicating one data element achieves an even number of data elements
Whether there is one transaction or a hundred thousand in a block, the merkle root always summarizes them into 32 bytes (Fig 7-4)
To prove that a transaction is in a block, a node makes log2(N) hashes including a merkle path connecting the transaction to the root
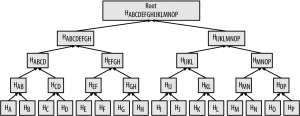
Figure 7-4. A merkle tree summarizing many data elements
A node proves K is included by merkle path consists of 4[blue]. With them any node proves HK is in the root by computing 4[dotted] (Fig 7-5)
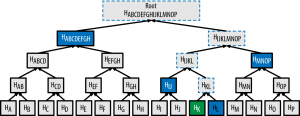
Figure 7-5. A merkle path used to prove inclusion of a data element
7-1 shows the process of creating a merkle tree from the leaf-node hashes up to the root. 7-2 is the result of compiling the merkle code
Example 7-1. Building a merkle tree
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
#include <bitcoin/bitcoin.hpp> bc::hash_digest create_merkle(bc::hash_list& merkle) { // Stop if hash list is empty. if (merkle.empty()) return bc::null_hash; else if (merkle.size() == 1) return merkle[0]; // While there is more than 1 hash in the list, keep looping... while (merkle.size() > 1) { // If number of hashes is odd, duplicate last hash in the list. if (merkle.size() % 2 != 0) merkle.push_back(merkle.back()); // List size is now even. assert(merkle.size() % 2 == 0); // New hash list. bc::hash_list new_merkle; // Loop through hashes 2 at a time. for (auto it = merkle.begin(); it != merkle.end(); it += 2) { // Join both current hashes together (concatenate). bc::data_chunk concat_data(bc::hash_size * 2); auto concat = bc::make_serializer(concat_data.begin()); concat.write_hash(*it); concat.write_hash(*(it + 1)); assert(concat.iterator() == concat_data.end()); // Hash both of the hashes. bc::hash_digest new_root = bc::bitcoin_hash(concat_data); // Add this to the new list. new_merkle.push_back(new_root); } // This is the new list. merkle = new_merkle; // DEBUG output ------------------------------------- std::cout << "Current merkle hash list:" << std::endl; for (const auto& hash: merkle) std::cout << " " << bc::encode_hex(hash) << std::endl; std::cout << std::endl; // -------------------------------------------------- } // Finally we end up with a single item. return merkle[0]; } int main() { // Replace these hashes with ones from a block to reproduce the same merkle root. bc::hash_list tx_hashes{{ bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000000"), bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000011"), bc::hash_literal("0000000000000000000000000000000000000000000000000000000000000022"), }}; const bc::hash_digest merkle_root = create_merkle(tx_hashes); std::cout << "Result: " << bc::encode_hex(merkle_root) << std::endl; return 0; } |
Example 7-2. Compiling and running the merkle example code
|
1 2 3 4 5 6 7 8 9 10 11 12 |
$ # Compile the merkle.cpp code $ g++ -o merkle merkle.cpp $(pkg-config --cflags --libs libbitcoin) $ # Run the merkle executable $ ./merkle Current merkle hash list: 32650049a0418e4380db0af81788635d8b65424d397170b8499cdc28c4d27006 30861db96905c8dc8b99398ca1cd5bd5b84ac3264a4e1b3e65afa1bcee7540c4 Current merkle hash list: d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3 Result: d47780c084bad3830bcdaf6eace035e4c6cbf646d103795d22104fb105014ba3 |
The efficiency of merkle trees becomes obvious as the scale increases. 7-3 shows the amount of data needs to be exchanged as a merkle path
Table 7-3. Merkle tree efficiency
This SPV (simplified payment verification) nodes use merkle paths to verify transactions without downloading gigabytes of full blocks
Merkle Trees and Simplified Payment Verification (SPV)
In order to verify a transaction is included, without downloading all the transactions, SPV nodes use an authentication path, or merkle path
A SPV node receives less than 1 KB of data for the block header and merkle path, more than a thousand times less than a full block (1 MB)